Problem

How to generate a series of points on sphere evenly?

• It is not easy as you think. Average distance on xyz or \(r\phi\theta\) cannot generate the point on a 2D circle or 3D sphere. They will very dense at polar. We will make an contrast between fibonacci spiral sphere and average walk pointing shpere.

• In order to quantify the sphere-like shapes of objects, we need to propose a method to describe the surface of the points on objects. We have an idea is that …

• If we can generate these equidistant points, we can define the energy distribute on the surface of sphere-like objects.

Fibonacci Squence & golden ratio

• A method based on a spiral walk of the spherical surface in angular increments equal to the golden angle. On mathematics, we call it The Fibonacci Sequence or Golden Ratio.

Golden Ratio

Golden Ratio is an Irrational Number(meaning we cannot write it as a simple fraction), like $ \pi $ and $ e $. The golden ratio grows from fibonacci squence. We can derive it from this formula: $\varphi = \frac{1}{\varphi}$

expanded formula:

$\varphi = \frac{1}{\frac{1}{\frac{1}{…}}}$

To solve this equation, we can get $\varphi$ is 1.61803…

Golden Angle

This the the golden angle looks like:

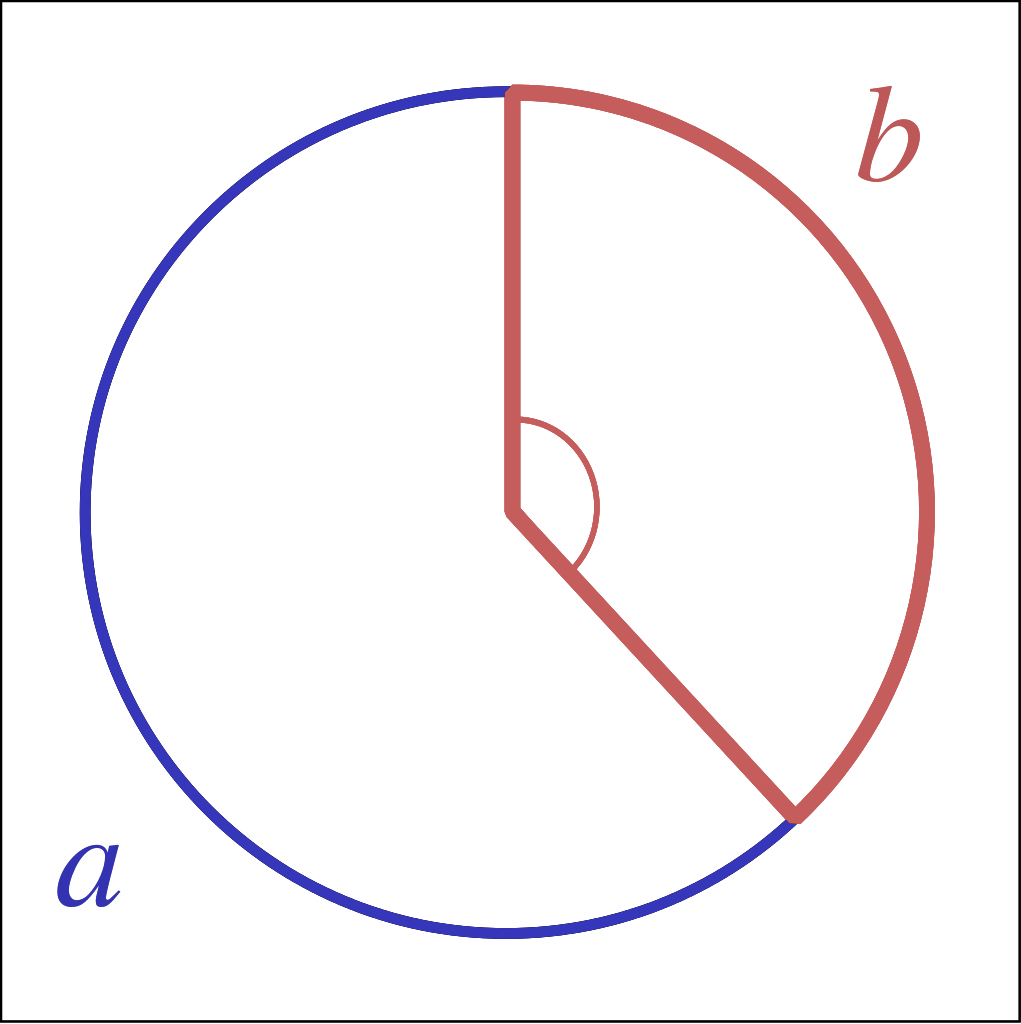
a and b satisfy the following relationship: $\frac{a}{b}=\frac{a+b}{b}:=\varphi$

so we get the golden angle b which is approximately 2.399963… radians or 123.50776… degress. We generate it in our program via $(3-\sqrt{5})*\pi$ .

Fibonacci Spiral Circle

Scattering the points evenly on a circle is not as easy as you think. Some methods like producing very large amount of random points on circles looks like a good ways. But we cannot control the number and cannot get average distribution.

Using Vogal’s Method we can generate a series of points distributing on circle evenly, which can combine the golden angle with an increasing radius $r$.

Here is my implementation:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
def fibonacci_spiral_disc(num_points, density_inverse=10):
    points = []

    phi = math.pi * (3. - math.sqrt(5.))  # golden angle in radians - 2.39999 radian (compared to degrees 137)

    for i in range(num_points):
        radius = math.sqrt(i) * density_inverse
        theta = phi * i  # golden angle increment
        x = math.cos(theta) * radius
        y = math.sin(theta) * radius

        points.append([x, y])

    return points

• Density_inverse means that the more density you want, this values should smaller.

Fibonacci Spiral Sphere

Like the fibonacci spiral circle, we want to find out a way to generate the points evenly on the sphere.

If the spiral starts at a sphere’s pole then the radius and circumference of the spiral at any point is proportional to $cos(lat)$ for $lat$ in $[-\pi/2,\pi/2]$ and the continuous distribution function (CDF) of the turns proportional to $sin(lat)+1$.

With this CDF, the point index $i$ of a latitude can be calculated with $i = \frac{N+1}{2}(sin(lat)+1) $ for $N$ the total number of points required. Then we can get $lat = arcsin(i\frac{N+1}{2}-1)$ .

Here is my code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
def XXX():
  points_cartesian = []
  points_spherical = []
  # https://bduvenhage.me/geometry/2019/07/31/generating-equidistant-vectors.html#:~:text=Summary,three%20points%20to%20the%20sphere.
  phi = math.pi * (3. - math.sqrt(5.))  # golden angle in radians - 2.39999 radian (compared to degrees 137)

  # latitude direction  pi ---?  polar angle ------from x, not from z
  # longitude direction 2pi  ---?azimuth angle

  for i in range(num_points):
      lat = math.asin(-1.0 + 2.0 * float(i / (num_points + 1)))
      # lat = lat % (-math.pi) if lat < 0 else lat % math.pi
      # lat = lat % (2*math.pi)
      lon = phi * i

      x = math.cos(lon) * math.cos(lat) * radius
      y = math.sin(lon) * math.cos(lat) * radius
      z = math.sin(lat) * radius

      points_cartesian.append([x, y, z])
      # points_spherical.append([radius, lat, lon])

  points_np_cartesian = np.array(points_cartesian)
  # points_np_spherical = np.array(points_spherical)
  return points_np_cartesian

Reference

1. https://www.mathsisfun.com/numbers/nature-golden-ratio-fibonacci.html

2. https://stackoverflow.com/questions/9600801/evenly-distributing-n-points-on-a-sphere/44164075#44164075

3. https://bduvenhage.me/geometry/2019/07/31/generating-equidistant-vectors.html

• Previous
  My undergraduate thesises
• Next
  數字貨幣交易記錄1